Deep Reinforcement Learning for Grid Scale Lithium-ion Battery Optimisation

Using Model-free DRL to Optimise Wholesale Energy Arbitrage for Grid-Scale Batteries

Oct 10, 2022

Introduction

As distributed generation becomes more prevalent in the energy mix and continues to protrude on traditional synchronous assets, the importance the effective optimisation of such technologies, is imperative to ensure adherence of the energy trilemma. Due to the smaller dispersed volumes on the grid and stackable revenue stream opportunities, batteries bring additional complexities to their optimisation from both a system operator’s and generator's perspective, with traditional techniques perhaps inhibiting optimisation and growth opportunities for the technology. Therefore, automated techniques particularly, from Machine Learning (ML) based algorithms, could be the most effective in maximising return by capturing the ever increasing volatility of the market, whilst also ensuring the continued opportunistic growth of the technology is further through efficient expansion. Ascertaining an effective control solution is further exacerbated by the revolution of market reform around such technologies, leading to the development of decentralised resources such as Virtual Power Plants (VPPs), an instrument that will continue to grow as companies such as Tesla plan to utilise it for grid scale integration of domestic batteries, further enforcing the necessity to have a digitised optimisation framework to produce robust optimisation approaches.

Start Date ➡️

Figure 1: Timeseries Performance of Grid-Scale (10MW/20MWh) Li-ion Battery Optimised with Double Dueling DQN Algorithm

This post endeavours to demonstrate the capabilities of data driven techniques by investigating the novel application of Deep Reinforcement Learning (DRL) to maximising the profit of a battery from wholesale energy arbitrage. Largely based on the codeless academic paper from Cao et al. (2019), the post looks to apply the deep Q-network (DQN) model introduced by DeepMind in 2015, as well as investigate some the improvements made to the basic architecture. Figure 1 shows the results from a 10MW/20MWh Li-ion battery optimised using a "Double Dueling" DQN method, more discussion around its performance will be given in the proceeding sections.

Environment

As Cao et al. (2019) highlights, incorporating the effects of battery degradation is a key component to deriving a successful arbitrage optimisation algorithm for lithium-ion batteries. In that, accurate accountability of degradation costs for associated actions is crucial to ensuring realistic profitability. Hence, a linear approximation of battery degradation has been incorporated into the model, helping to further legitimise the approach by invoking a practical perspective to the optimisation. In this model, a hypothetical capacity degradation curve has been created to determine the resultant degradation cost on a per cycle basis. A degradation coefficient is taken forward into the reward formulation for the problem, as determined by:

\begin{equation} \alpha_{d,j} = \frac{E_{s,j} - E_{c,j}}{\sum_{i=1}^{T}|P_{e,t}| \cdot C_{B}} \end{equation}

Where \({E_{s,j}}\) and \({E_{c,j}}\) are the nameplate battery capacities at the start and end of episode \({j}\), \({P_{e,t}}\) is the battery charge or discharge in kWs and \({C_{B}}\) is the per unit capital cost of the battery in terms of capacity (£/kWh)

The battery model helps to add further degrees of practicality to the problem by invoking a steady state circuit model representation for calculating lithium-ion battery efficiency, creating a non-linear approximation of efficiency for each timestep relative to the current action and SoC (state-of-charge), a variable that is often assumed to be steady-state in most other models. The charging and discharging efficiencies relative to respective power and SoC are visualised in figure 2, for further details on calculation refer to either Cao et al. (2019) or the coded implementation on github.

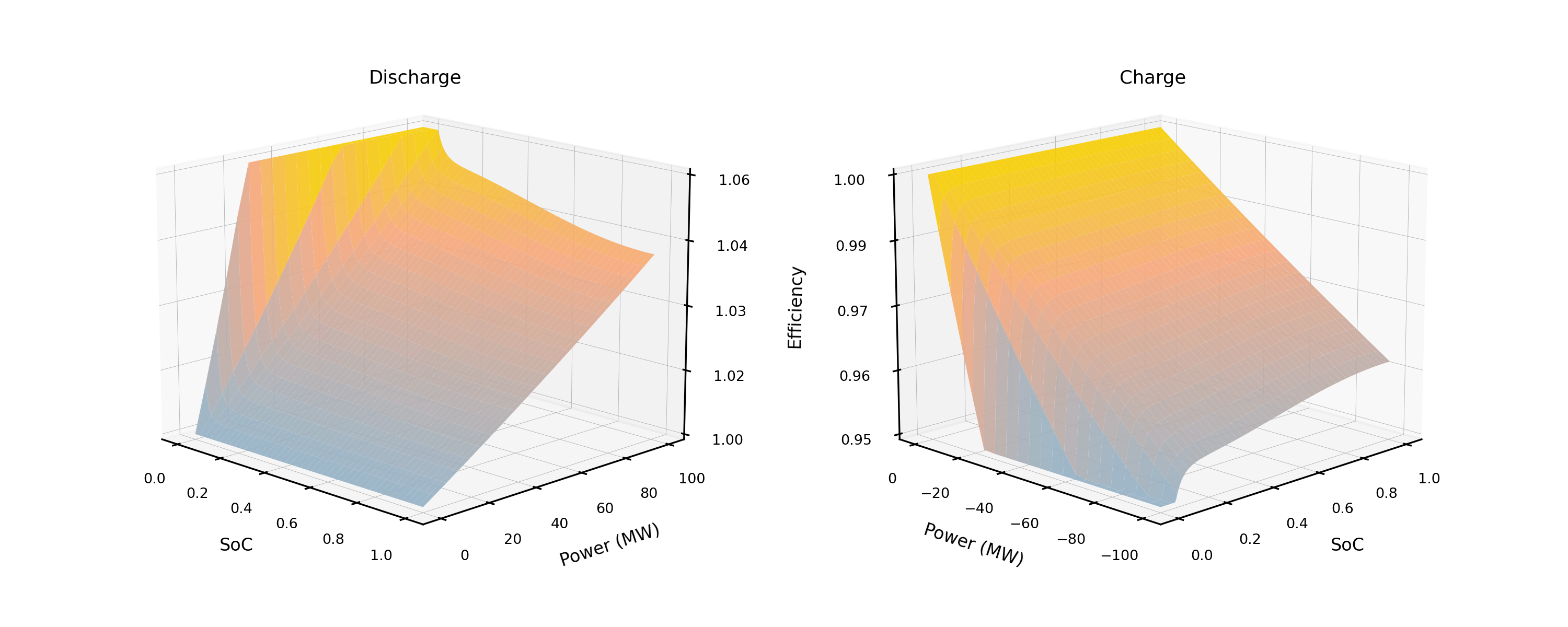
Figure 2: Charge and Discharge Efficiency of Li-ion Battery with Respect to SoC and Power

The aforementioned methodologies for degradation and efficiency help to accentuate the approach to this investigation and helps to provide a compelling application for DQN. The battery behaviour is dictated by a generalised mathematical model, ultimately determining the constraints for the actions of the agent, the conditions are as shown below:

\begin{equation} SoC_{t+1} = \begin{cases} SoC_{t} - \frac{1}{E_{ess}} \cdot \eta_{t}^{ch} \cdot \int_{t}^{t+1} \ P_{e,t} dt, P_{e,t} < 0 \\ SoC_{t} - \frac{1}{E_{ess}} \cdot \frac{1}{\eta_{t}^{dis}} \cdot \int_{t}^{t+1} \ P_{e,t} dt, P_{e,t} > 0 \\ SoC_{t} - \frac{1}{E_{ess}} \cdot \int_{t}^{t+1} \ P_{standby,t} dt, P_{e,t} = 0 \\ \end{cases} \end{equation}

Where \({SoC_{t}}\) is the sate-of-charge at timestep \({t}\), \({E_{ess}}\) is the energy capacity of the battery, \({P_{e,t}}\) is the power of the battery at the timestep, in which \({P_{e,t}} > 0\) when discharging and \({P_{e,t}} < 0\) when charging. \(\eta_{t}^{ch}\) and \(\eta_{t}^{dis}\) are the charge and discharge efficiencies respectively. The episodic formulation of the optimisation was centred around a 168-hour time horizon examined at an hourly resolution. In which, the proceeding 24-hour price track along with the current \({SoC}\) at timestep \({t}\) formulates the state space:

\begin{equation} state\_space_{t} = (c_{t}, c_{t+1} ... c_{t+22}, c_{t+23}, SoC_{t}) \end{equation}

The action space has been discretised into five possible actions: (\({-P_{e}^{max}, -0.5P_{e}^{max}, 0, 0.5P_{e}^{max}, P_{e}^{max}}\)), with a further physical constraint limiting the actual power charge or discharge relative to the current \(SoC\), a methodology used to protect against excessive depth-of-discharge and maintain battery longevity, as expressed by:

\begin{equation} \frac{(SoC_{t} - SoC_{max}) \cdot E_{ess}}{\eta_{t}} \leq P_{e,t} \leq \frac{(SoC_{t} - SoC_{min}) \cdot E_{ess}}{\eta_{t}} \end{equation}

Where \({P_{e}^{max}}\) is the original rated capacity of the battery. In order to appropriately guide the agent, reward formulation is an imperative component to ensuring the successful optimisation of the problem. For the energy arbitrage problem, cumulative profit is of utmost concern. Hence, the reward function has the capability of being positive and negative over each timestep, encouraging the agent to take actions that lead to the increased cumulative profit over the course of an episode. As previously highlighted, the profit has to also incorporate the defined degradation coefficient, ensuring the appropiate cost is accounted for at each timestep. The resultant reward function is therefore:

\begin{equation} R_{t} = c_{t} \cdot P_{e,t} - \alpha \cdot |P_{e,t}| \end{equation}

The formulation of the problem further extends the practical insight to the application of DRL by adding price forecasting capabilities to the environment. In an actualised environment, the DQN agent would not have perfect foresight of the 24hr price track, therefore a Pytorch model to make predictions based off the previous 7-day, hourly, prices was integrated into the environment allowing for the optimisation to be conducted relative to the idealised true forecast basis, as well as with regard to the forecasted prices from the Pytorch model. The forecast model is composed of a CNN and LSTM and was trained on 3-years of data (2015-2017 inclusive) and tested on 2018 prices and after minimal hyperparameter training, a MAE of ~£6.90 was observed, for a further insight into model architecture and input features refer to the code repository. Performance of both cases are analysed in the results section of the post.

Mixed Integer Linear Programming (MILP)

In order to provide a basis for comparison a Mixed Integer Linear Programming (MILP) optimisation was also composed for the problem, although the dynamic efficiency derivation was eliminated from this linearised approach, the constraints and objective function helps to garner insight to the opportunities for DRL, as we'll come to see later in the post. Pyomo with GNU linear Programming Kit (GLPK) provided the framework to solve the MILP problem, an overview of MILP approach is given here but for an exhaustive breakdown of the MILP methodology, including reference to all constraints, it is recommended that the reader refers directly to the code repository. For the most part the problem is formulated around the same boundary conditions as latterly explored for the DQN model, with the objective function defined as:

\begin{equation} obj = \sum_{t=1}^{N} (c_{t} \cdot E_{out} \cdot \eta_{dis}) - (c_{t} \cdot E_{in} \cdot \eta_{ch}) - \alpha \cdot (E_{out} - E_{in}) \end{equation}

Due to the nature of the MILP optimisation, the framework could allow the battery to simultaneously charge and discharge hence additional bounds have to be specified, in this case the bigM method has been adopted to ensure that it is not possible to charge and discharge within the same time period, for further information regarding this approach please refer to Barbour (2018)

DQN Agent

A full description into the background and operation of the DQN algorithm is outside the realms of this blog post. However, a high-level overview of the algorithm focusing on the implemented extensions to the basic DQN algorithm that have been explored is given. A baseline comparison has also been made through the development of a Mixed Integer Linear Programming (MILP) algorithm, allowing for further demonstration of the capabilities even for the baseline (vanilla) DQN configuration. As with the price forecasting model, the DQN agent was implemented in Pytorch, with all training conducted under a Google Colab Pro+ subscription. The vanilla DQN implementation in this post, deviates from that of Cao et al. (2019) in that a "soft update" technique was used to partially update weights of the target network more frequently during training, helping to promote the stability of learning apposed to the traditional "hard update" methodology, which helped with train time and promoted more stable tuning of the update parameters. The explored iterations build upon the soft update baseline of the vanilla DQN algorithm, including:

Double Dueling DQN: To compact the tendency of a vanilla DQN optimisation from overestimating \({Q}\) values which can lead to suboptimal policies being derived during training due to inherent max operation of strategy of the conventional Bellman equation. A full derivation will not be given here but effectively, the 'double' update refers to the amendment to the Bellman equation in which the next action is taken from the trained network whereas the \({Q}\) values are taken from the target network negating the influence of overestimation and ensuring a more optimal solution is achieved. The 'dueling' updates look to further improve the accuracy in associating \({Q}\) values for a state action pair by dividing the approximation of the value into quantities comprising of the state value (\({V_{s}}\)) and the advantage of the actions in this state (\({A_{s,a}}\)). These updates in combination with the latter deuling changes help to further increase training stability and promote the likely hold of increased performance.

Noisy Networks DQN: In the conventional DQN approach exploration of the action state space is achieved through the epsilon greedy methodology, which enforces random exploration that depletes as training progresses through episodes. Alternatively, the epsilon greedy methodology can be replaced by adding noise to the fully connected layers of the DQN network and adjust the parameters of the noise with backpropagation during training. This approach has been shown to drastically improve train time.

Double Dueling with Noisy Networks DQN: Also explored but omitted from the comparison due to anomalies and instability in the resultant reward profile observed during training, this has been attributed to inadequate hyperparameter tuning and as such retained in the code repository for opportunities to further investigate.

This study looks at the case of a 10MW, 20MWh (2hr) battery and although this may be considered an unrealistic case for a standalone grid connected battery, the model and code is suited to investigating any configuration. The DQN agent is exclusively trained on 1-year of UK wholesale market data (2018), in which the price track is consistently reset during the episodes. The trained DQN agents were tested and compared on the wholesale prices for 2019 and will be discussed in the proceeding results section.

Results

The training reward profiles for the DQN algorithms are illustrated in figure 3. A marginal improvement in reward out-turn and rate of convergence can be observed between the vanilla and double dueling implementations. This may reflect the standard vanilla DQN's capability to optimise the scenario, as it would be expected that such updates would result in a more accentuated uplift. Advances in learning stability may also be obscured by the soft-update methodology inherent in the baseline scenario. The noisy networks architecture prevails as the most efficient, in terms of training, reaching convergence almost 4000 episodes before the other DQN frameworks, the noisy exploration strategy also shows a reward attainment similar to that of the double dueling DQN algorithm. The cyclic training around the 1-year of training data can also be observed from the uniform volatility evident, for all approaches, after convergence.

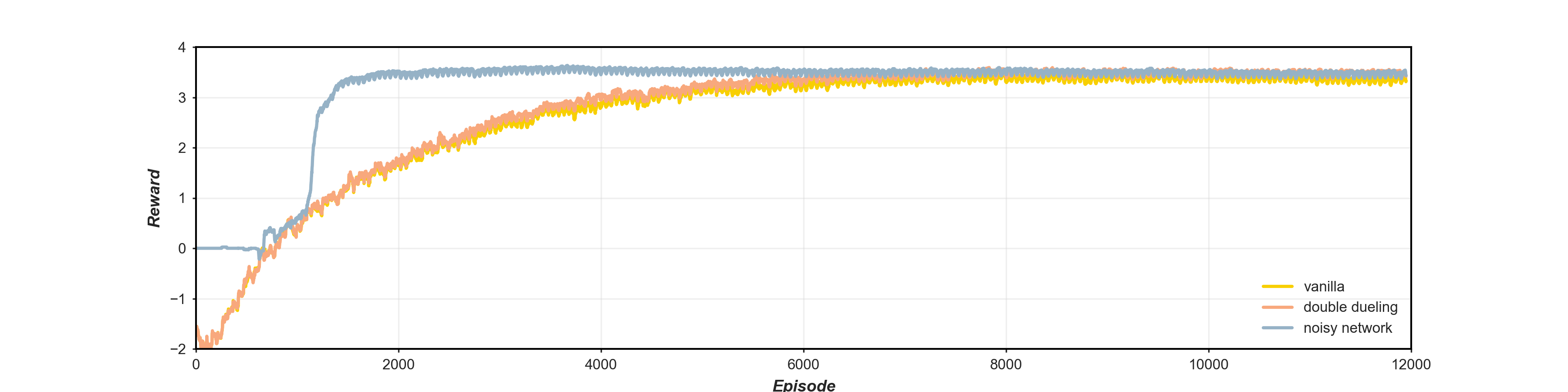
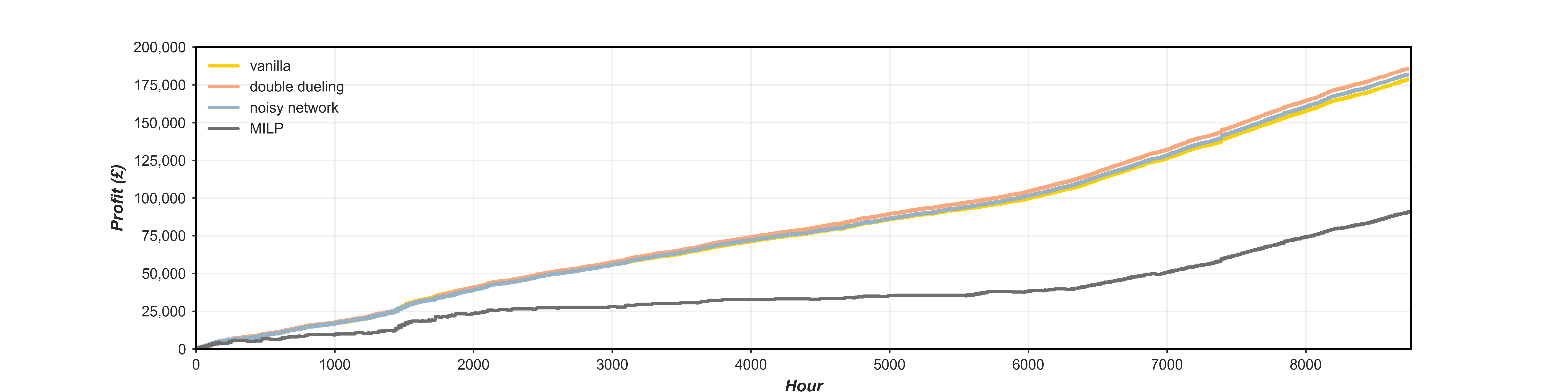
Figure 3: Training Reward Performance for DQN Agents (50 episode rolling average)

Figure 4 depicts the cumulative profit for each of DQN iterations over the 2019 inference period along with the performance of the MILP model for the same period. With a ~95% uplift in cumulative profit observed between the baseline MILP and vanilla DQN performance, the opportunity of DRL is made evident. The divergence in which the extensions to the DQN baseline become more evident in terms of their uplift in cumulative profit is in the latter section of the year which could be an indication of the algorithm's ability to better recognise the variation in degradation costs over time, with double dueling prevailing as the most lucrative performer in terms of cumulative returns. The timeseries performance of the double dueling algorithm over the inference period are given in figure 1, it can be observed that the optimisation can fail to capture the definitive peaks and troughs for a given period, reflecting the opportunity for further refinement and possibility of other DQN extensions and DRL techniques. It was found that during training, the outturn of the best update was susceptible to the utilised training year, in that following the same strategy and training data outlined by Cao et al. (2019) the noisy network extension outturns more profitable than the other extensions.

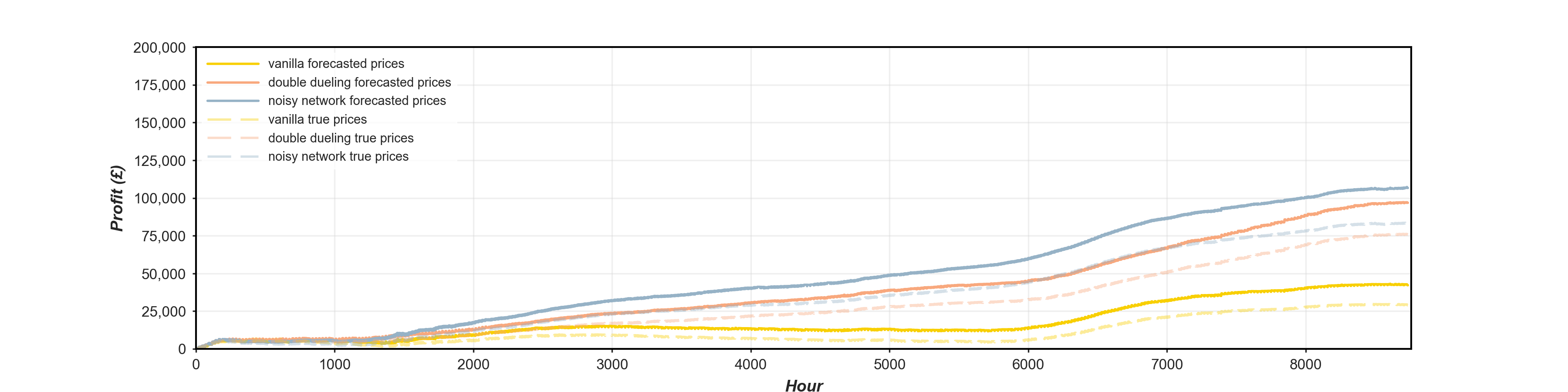
Figure 4: Cumulative Profit Comparison Inference Year (2018)

The discussion to now has been centred on the operation of the environment under a perfect price scenario. To try infer further degrees of realism to the study, the DQN inference was also carried out relative to a forecasted price track. Figure 5 illustrates the performance of each of DQN algorithms for forecasted prices giving the actualised cumulative profit relative to both the underlying true out-turned prices as well as the forecasted prices themselves. In all scenarios it shows a significant downturn in profits. Ideally, the DQN would be trained in conjunction with the forecasting model to better maximise performance, a possible note for further work.

Figure 5: Cumulative Profit Comparisons for Forecasting Environment over Inference Year (2018)

Conclusions & Further Work

The post serves as an insightful demonstration to the potential of DRL techniques to the battery optimisation problem. Even with the modest levels of hyperparameter tuning adopted in this study, we see the opportunities for the uplift in performance compared to other notable techniques such as seen with MILP. The degradation model and forecasting capabilities integrated into the optimisation help to bring further degrees of realism to the study and additional novelty for the comparison. Furthermore, the extensions of the DQN explored help to convey the additional opportunities for increased performance. Some identified opportunities for further work and retification of known limitations, include:

Imply battery sizing during training of DQN model -possibly within the state space- to allow for easier manipulation of configuration scenarios during inference.
Investigate opportunities to integrate stackable revenue streams, particularly those from balancing mechanism into the DRL learning process.
Opting for a different DRL architectures could allow for the adoption of a continuous action space which could bring about further opportunities for refined performance.
Pursuit of temporally higher resolution data to better capture market volatility and arbitrage opportunities for batteries.