Probabilistic Forecasting of Renewable Generation & Wholesale Prices with Quantile-Regression
Sequence-to-Sequence Networks with Spatial-Temporal Attention to Forecast Day-Ahead UK Power Generation and Wholesale Auction Prices
Jun 15, 2022
Introduction
With the 2022 UK energy security strategy anticipating to further accelerate the development of offshore wind capacity to 50GW by 2030, alongside solar capacity potentially quintupling by 2035, the importance of increasing energy forecasting accuracy is ever growing. As power generation moves away from traditional synchronous assets, becoming increasingly decentralised and heterogenous, accurate forecasting is not only pertinent for the system operator to sustain the security of the network, but the intermittency of renewable generation is expected to result in volatile market conditions, especially in the short term, making it a lucrative tool for maximising economic return. This post looks to demonstrate the capability machine learning methods to predicting solar, wind, demand and wholesale power prices for the day-ahead (DA) stage.
The performance of supervised deep neural networks, applied to timeseries forecasting, are explored as part of this post. Investigating the performance of more traditional recurrent neural networks to novel encoder-decoder based architectures. The methods explored here are not seen as direct alternatives that could supersede existing techniques but rather act as an introduction to machine learning based methods and highlight their potential when applied to the forecasting problem.
There are many ways to approach the forecasting problem, varying between end-user requirements. In order to effectively portray the inherent uncertainty of the forecasts, probabilistic representations over the forecast horizon have become the expected standard throughout the industry, allowing traders and system operators alike to identify the potential variability of a value over time and although deterministic values may be relied upon to fill positions, the narrative of these values can be better understood. This post demonstrates the use of deep learning techniques in combination with quantile regression to produce probabilistic forecasts. Figure 1 depicting the consecutive DA quantile forecasts for each of the investigated variables over one week, with further quantification and discussion given on the forecast performance given in the results section in this post.
Data Selection & Processing
The approach to formulating the model was predominately centred around the desire to investigate the use of spatial and temporal attention mechanisms in relation sequence-2-sequence recurrent neural networks. In order to incorporate such mechanisms to the model, 2D variable data was used as the main source for the model, with various Numerical Weather Prediction (NWP) model providers investigated as part of the initial appraisal. Ideally, high resolution data with practical application was sought, such as from the UK Met Office Atmospheric 2km Deterministic model, however it became quickly apparent that although the dataset would enable the practical collection of forecasted NWP parameters on a daily basis, the historic data, necessary for supervised learning, requires payment. The computational and fiscal expense associated with dataset was determined unnecessary for the novel exploratory objectives for this blog post. With further investigation it was apparent that the desire to attain a practical application of model was only possible through expenditure, as such the desire to attain this objective was abandoned for aforementioned reasons.
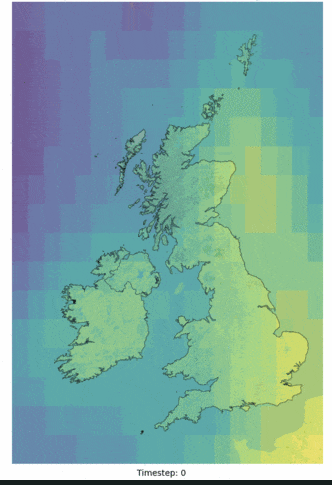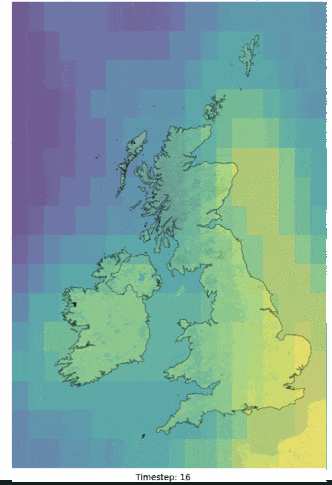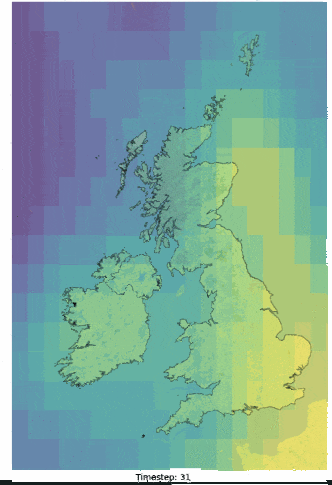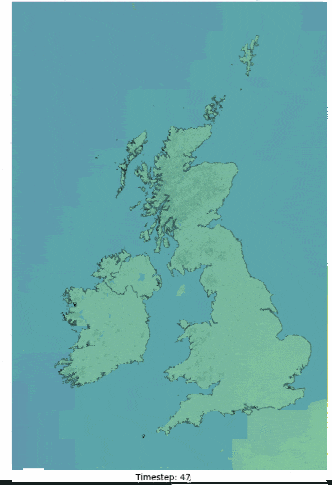
Although an impractical application, the ECMWF (European Centre for Medium-Range Weather Forecasts) ERA5 reanalysis dataset was adopted for this work. The ERA5 data is available at a 5-day latency, at an hourly 3km resolution and covers a range of variables that showed reasonable corelations to the labelled parameters being investigated. Figure 3 illustrates an example of a raw ERA5 variable over one day (low cloud cover), interpolated to 48 half hour periods (HH) figures helps to illustrate the catchment area adopted for this investigation. Furthermore, ERA5 data is often a precursor to many forecasted NWP models and as other practical 2D datasets will be similar in structure, the methods adopted as part of the post, could in theory, be applied to a more practical inference scenario where forecasted NWP parameters are available. In combination with variable ERA5 features, data engineering was utilised to better infer temporal dependencies in the model.
To maximise design iterability, the windowing of NWP and temporal features was handled by a customised Keras data generator (shown in the code snippet below) capable of varying the 2D features and labels into user specified input and output horizons. From high level appraisals, it was found that the previous 336 HH periods as the input horizon showed reasonable performance in the trade-off between model accurate and training time when forecasting the proceeding 48 HH periods. Unfortunately, due to this data generation configuration, it does make it difficult to effectively shuffle the data during training. However, the benefit retained by the variability of forecasting horizon was seen to outweigh such concerns for a novel and exploratory study such as this one.
# as adapted from: https://stanford.edu/~shervine/blog/keras-how-to-generate-data-on-the-fly
class DataGenerator(tensorflow.keras.utils.Sequence):
def __init__(self, dataset_name, x_length, y_length, hidden_states, batch_size, shuffle):
self.dataset_name = dataset_name
self.batch_size = batch_size
self.shuffle = shuffle
self.n_s = hidden_states
self.xlen = x_length
self.ylen = y_length
self.index_ref = 0
self.on_epoch_end()
def __len__(self):
# 'number of batches per Epoch'
return int(np.floor((self.ylen - input_seq_size - (output_seq_size-1)) / self.batch_size))
def __getitem__(self, index):
# input and output indexes relative current batch size and data generator index reference
input_indexes = self.input_indexes[(index*self.batch_size) : (index*self.batch_size) + (self.batch_size + (input_seq_size-1))]
output_indexes = self.output_indexes[(index*self.batch_size) + input_seq_size : (index*self.batch_size) + input_seq_size + (self.batch_size + (output_seq_size-1))]
# Generate data
(X_train1, X_train2, X_train3, X_train4, s0, c0), y_train = self.__data_generation(input_indexes, output_indexes)
# replicate labels for each quantile
y_trues = [y_train for i in quantiles]
# extend true values for spatial and temporal attention (only relavant if compiled model used for inference)
# y_trues.extend([[], []])
return (X_train1, X_train2, X_train3, X_train4, s0, c0), (y_trues) # pass empty training outputs to extract extract attentions
def on_epoch_end(self):
# set length of indexes for each epoch
self.input_indexes = np.arange(self.xlen)
self.output_indexes = np.arange(self.ylen)
if self.shuffle == True:
np.random.shuffle(self.input_indexes)
def to_sequence(self, x1, x2, x3, x4, y):
# convert timeseries batch in sequences
input_start, output_start = 0, 0
seqX1, seqX2, seqX3, seqX4, seqY = [], [], [], [], []
while (input_start + input_seq_size) <= len(x1):
# offset handled during pre-processing
input_end = input_start + input_seq_size
output_end = output_start + output_seq_size
# inputs
seqX1.append(x1[input_start:input_end])
seqX2.append(x2[input_start:input_end])
# outputs
seqX3.append(x3[output_start:output_end])
seqX4.append(x4[output_start:output_end])
seqY.append(y[output_start:output_end])
input_start += 1
output_start += 1
# convert to numpy arrays
seqX1, seqX2, seqX3, seqX4, seqY = np.array(seqX1), np.array(seqX2), np.array(seqX3), np.array(seqX4), np.array(seqY)
return seqX1, seqX2, seqX3, seqX4, seqY
def __data_generation(self, input_indexes, output_indexes):
# load data for current batch
f = h5py.File(f"../../data/processed/{model_type}/{self.dataset_name}", "r")
X_train1 = f['train_set']['X1_train'][input_indexes] # main feature array
X_train2 = f['train_set']['X2_train'][input_indexes] # input time features from feature engineering
X_train3 = f['train_set']['X3_train'][output_indexes] # output time features from feature engineering
# no spatial data if model is training for price forecasting
if model_type != 'price':
X_train4 = f['train_set']['X1_train'][output_indexes][:,:,:,1:] # all nwp features apart from the generation itself
X_train4 = np.average(X_train4, axis=(1,2))
else:
X_train4 = f['train_set']['X1_train'][output_indexes][:,1:]
y_train = f['train_set']['y_train'][output_indexes]
f.close()
# convert to sequence data
X_train1, X_train2, X_train3, X_train4, y_train = self.to_sequence(X_train1, X_train2, X_train3, X_train4, y_train)
s0 = np.zeros((self.batch_size, self.n_s))
c0 = np.zeros((self.batch_size, self.n_s))
return (X_train1, X_train2, X_train3, X_train4, s0, c0), y_train
Minimal cleaning was conducted against the data, mainly a rudimental elimination was preformed to remove periods of curtailment from the wind labels. Entire days were removed from the data set when a “nan” values were present. To negate anomalies on the datasets (mainly price and demand) imposed by the coronavirus pandemic, the span of the collected data runs from 2017-2019 inclusively. In an attempt to include seasonal variability in the test set, the last ~20% of the data is retained for testing.
Model Architectures
Figure 2 illustrates the high-level schematic of the novel encoder-decoder architecture explored as part of this study. Developed in Keras, the modelling strategy endeavoured to increase exploration and iterability, maximising the potential learnings from the project. To better appreciate the performance of the resulting model, which contains both spatial and temporal attention mechanisms, additional model architectures were investigated helping to establish further baselines to the comparison and more readily commentate on the inclusion of particular aspects of the model. These architectures start from the most basic in the line of comparisons, where a single Bidirectional layer is used to predict the output forecast window, this built upon to create a vanilla encoder-decoder model (seq2seq) in which the temporal and spatial attention mechanisms are added cumulatively to create a further basis of comparison, as well as the objective model for this study. A Bidirectional LSTM was adopted for all encoder architectures, due to the work carried out by Toubeau et al. (2018) highlighting the increased accuracy from the availability of the forward and backward hidden weights of the LSTM layer. A detailed introduction to Recurrent Neural Networks (RNNs) and the architectures utilised here are deemed outside the scope of this post but notable sources are given in resources section.
In order to achieve the effective derivation of all preferred quantiles in the model, a separate decoder is produced over each quantile the user specifies, which enables the association of a different loss functions for each of the quantile outputs. In this case, the replicated loss function is the quantile (or pinball) loss, which lends itself well to supervised deep learning problems as the minimisation of such a function yields the resulting quantile for the problem. The below code snippet gives the pratical application of the pinball loss for Keras, where the "y" is the true value, "f" is the prediction and "q" is the quantile of concern (i.e. the probability for an observation to a distribution to be below this value, expressed as a value between 0-1, notably when q=0.5, the loss function equates to Mean Absolute Error (MAE)):
# define loss for each quantile
q_losses = [lambda y,f: K.mean(K.maximum(q*(y - f), (q-1) * (y - f)), axis = -1) for q in quantiles]
Training for all models was carried out in a Google Collaboratory notebook, predominately running on a 54.8GB RAM with a 16GB Tesla V100 GPU instance, in which the most complex model containing the spatial attention mechanism, simultaneously providing outputs over all quantiles and trained over 20 epochs, resulted in a ~18hr train time.
Results
In order to provide a comparative breakdown both probabilistic and deterministic metrics have been provided against the performance of each model. As latterly mentioned, as central quantile is equivalent to the MAE, hence further comparison is possible to the deterministic values of a simple daily persistence forecast, as well as the Transmission System Operator (TSO) day-ahead forecast for each variable. Both MAE and root-mean-square error (RMSE) are presented on this basis. Although this does deviate from the objective of producing and benchmarking probabilistic forecasts, the RMSE and MAE does provide further interest to the comparison. To better compare the Prediction Intervals (PI) produced by the quantile regression of each deep learning model, the Prediction Interval Coverage Probability (PICP) metric was used to evaluate the reliability of the produced intervals, specifically for a PI of 90% in the case of table 1. The formula for PICP is as:
$${ PICP = \frac{1}{N} \sum_{i=1}^N c_{i}} $$ Where \({N}\) is the number of test samples and \({c_i}\) is an indicator defined as:Where \({y_{i}}\) is the true value of a prediction and \({L_{q}}\) and \({U_{q}}\) are the lower and upper boundary limits of the PI of interest respectively. Further metrics eliminated in this post but incorporated in the code are given by Bazionis & Georgilakis (2021).
| Solar | Wind | Demand | Price | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| PICP | MAE | RMSE | PICP | MAE | RMSE | PICP | MAE | RMSE | PICP | MAE | RMSE | |
| Persistence | - | 375.8 | 834.8 | - | 2255.0 | 2924.3 | - | 2044.2 | 2776.3 | - | 5.12 | 7.03 |
| Bi-directional LSTM | 92.11 | 327.4 | 689.2 | 87.84 | 1318.7 | 1760.6 | 91.44 | 1459.8 | 1903.2 | 72.45 | 6.39 | 8.05 |
| Seq2Seq | 96.09 | 300.5 | 655.2 | 94.80 | 937.0 | 1251.3 | 90.84 | 1315.0 | 1715.2 | 46.47 | 5.75 | 7.19 |
| Seq2Seq with Temporal Attention | 98.10 | 291.1 | 613.9 | 90.10 | 998.1 | 1320.7 | 86.71 | 1457.6 | 1890.3 | 80.18 | 6.53 | 8.48 | Seq2Seq with Temporal & Spatial Attention | 95.27 | 271.0 | 585.2 | 85.48 | 1062.1 | 1383.1 | 70.21 | 1519.5 | 1903.4 | - | - | - |
| TSO DA Forecast | - | 141.0 | 289.2 | - | 1141.0 | 1440.4 | - | 2397.3 | 3560.8 | - | - | - |
The intricacies involved in investigating the performance of a probabilistic forecast are apparent from table 1, with variability observed between probabilistic and deterministic benchmarks for a number of variables over intended model performance increases. DA solar generation forecasting does however show the incremental performance increases over each model iteration, when considering the daily persistence forecast as a baseline, as would be hypothesised, especially when considering MAE and RMSE. However, even with the introduction of both temporal and spatial mechanisms performance is still out-with that of what is capable by the TSO. Contrary to what is observed for the wind and demand forecasting models, where even the more basic iterations of the model show increased performance against the TSO forecasts for the test samples. Furthermore, the introduction of the temporal and spatial attention mechanism shows to lessen performance for these variables, perhaps less of a surprising revelation in the case of wind forecasting where temporal weighting may be less of a prevalent feature but especially surprising in the case for demand forecasting possibly highlighting issues in the fundamental architecture of the model. The irrelevance of the spatial correlations of the selected input features to the wind and demand labels are more expected principally from the coarseness and correlations of the 2D data to the wind and demand labels when compared to that of the performance of the solar model.
Although the sequence-to-sequence models show better performance when compared to the attention model counterparts in the cases of wind, demand and price DA forecasting, abnormalities in resultant PIs are apparent, including volatile and overlapping quantile predictions, an issue that could be resolved with further hyperparameter tuning. Hence, all weekly consecutive forecast examples, portrayed in figure 1 therefore show case the performance of the relevant attention-based sequence-to-sequence model for each model. The PICP helps to quantify the reliability of PI, in this the case the 90% PI, however sharpness of PIs is also an important metric that helps to build confidence in predictions. Although not quantified in this post, from observing the results in figure 1 there appears to be large differences in lower and upper PI intervals, particularly in the case of the solar generation forecasts, which could again be due to poor correlation and sparsity in feature variables to labelled data.
Due to the exploratory nature of the work carried out here, a couple of attention mechanisms were examined to investigate their influence on model accuracy. An example of the spatial attention weights derived in the prediction of a DA solar forecast is illustrated in the figure 4, where it can be observed that greater model attention is given to south-eastern section of the UK. Although this contradicts the higher density of solar PV installations (mainly south-west), the model does show promise in identifying potential areas of interest, especially considering the attention fades and becomes homogeneous during non-daylight hours.
Examples of temporal attentions, for each variable, are illustrated in figure 5. Generally, among all variables, the temporal attention mechanism assigns a higher degree of focus to the previous daily values. Ideally, it was hypothesised that the model would recognise the most pertinent NWP features from the input sequence, rather as demonstrated for the solar attentions, the mechanism is continuously drawn to the previous day irrelevant to the current NWP provided for the forecasted day, highlighting the model’s propensity to solely focus on the temporal features of the input sequence. Temporal weights for demand and price do show inclinations of further variation but as quantified in table 1, fails to provide a consistent mechanism capable of reflecting a notable uplift in model accuracy. As for the attention generation, the example illustrated in figure 5 is consistent among most predictions, in that the model attentions vary little and focus is given to the last few hours of the input sequence.
Conclusion
Although the novel attention-based sequence-to-sequence model failed to prevail consistent increases in test set accuracy across all variables, the potential of these concepts, in particular RNNs, is still highlighted through promising performance gains when compared to those provided by the TSO. The models and concepts investigated in this post can not only be considered novel in their practical application of the forecasting problem but are becoming dated concepts, especially with the advent of alternative model architectures such as transformers, help to address some of the key fallacies of RNNs and particularly LSTMs. Gradient Boosted Trees (XGBoost) have demonstrated their competence in the forecasting problem, these alongside other advancements will be investigated in future blog posts.
The post helps to highlight the intricacies in model performance when benchmarking probabilistic forecasts and ultimately due to the decision to pursue lesser quality data and divert time away from appropriate pre-processing and cleaning, the quality of results and forecasted quantiles were inherently inhibited from the outset of the study. Nonetheless, promising results were observed among all investigated variables, apart from those of the DA wholesale price forecasting model. The work demonstrates the practical capability of attention mechanisms and the opportunities for encoder-decoder architectures in the probabilistic forecasting problem, the work here will be built upon in further blog posts to build further narrative on the problem and hopefully provide practical results. For further insight into the application of ML to the forecasting problem, it's recommended that the reader checks out the work being done by Open Climate Fix into Solar Nowcasting - here
Lessons Learned
As reiterated throughout the post, the premise of the work carried out here is novel and exploratory, deterred from the aim of practical application and rather focused on providing a framework that highlights the potential and approach that the application of sequence-to-sequence models has to probabilistic forecasting. Some of the key learnings and identified shortcomings from study include:
- Disproportionate amount of attention paid to creation of deep learning architecture, rather than pre-processing of data including cleaning, largest increases in model accuracy could have been captured from well correlation, clean data.
- Instability between the two attention mechanisms observed during training, in particular spatial attention weights often showed to struggle to convey any variation when combined with the temporal attention mechanism.
- Demonstrated use of Keras API with “in-built” many-to-one architecture and associated inference strategy, perhaps an unnecessary use case of the high-level API and rather project may have benefited from the application of more fundamental use cases such as Tensorflow or Pytorch.
- Ability of Data Generator to shuffle dataset during training could be seen as an additional benefit to increase model accuracy.
- Constraints added by the handling of 2D spatial data make it difficult to preform effective hyperparameter tuning.
- Insightfulness of study could be broadened by analysing additional ML architectures alongside the variations of RNNs examined here.
Resources
- https://www.elexon.co.uk/documents/training-guidance/bsc-guidance-notes/bmrs-api-and-data-push-user-guide-2/
- https://open-power-system-data.org
- https://stanford.edu/~shervine/blog/keras-how-to-generate-data-on-the-fly
- https://cds.climate.copernicus.eu/cdsapp#!/dataset/reanalysis-era5-pressure-levels?tab=overview
- https://colah.github.io/posts/2015-08-Understanding-LSTMs
- https://blog.keras.io/a-ten-minute-introduction-to-sequence-to-sequence-learning-in-keras.html
- https://colab.research.google.com/github/kmkarakaya/ML_tutorials/blob/master/seq2seq_Part_D_Encoder_Decoder_with_Teacher_Forcing.ipynb
_animation.gif)