Reinforcement Learning for Offshore Wind Farm Optimisation
Applying Q-Learning to Static & Quasi-Dynamic Offshore Wind Farm Environments to Optimise Wake Steering Strategies
Apr 30, 2022
Introduction
This post is based on the conference paper published by NREL, and with no publicly available coded implementations, work was done to replicate some of the key components of the paper. The use case demonstrates the potential of how even rudimental Reinforcement Learning (RL) techniques can be applied to such control problems and can lead to an improvement in performance when compared to traditional optimisation techniques.
The post applies RL to optimise offshore wind farm power yield through the optimisation of a wake steering strategy, the practice of intentionally misaligning turbine yaws to deflect wakes away from downstream turbines. Although a partial implementation of the paper, the post covers an overview of the background and set-up highlighting specific learnings from the replicated implementation. For a more comprehensive insight, it is recommended that the reader refers back to the original paper from NREL.
The problem applies a Multi-Agent-System (MAS) using NREL's Floris as a foundation to the environment, which is a control-oriented model traditionally used to investigate steady-state wake interactions in wind farm layouts. The turbines, or agents, are optimised independently of one another, using separate Q-learning algorithm for each agent with the mutual objective to promote the overall wind farm power. The optimised RL wake-steering strategy results in a 12.4% increase in total wind farm output over the baseline comparison relative to one direction sector (270°), this is a further 1% improvement in comparison to Floris' preferred in-built optimisation method. This may seem to be a marginal improvement but relative to the increasing rated capacity of offshore windfarms, 1% could represent a substantial revenue gain.
It should be noted that the code is not a like-for-like implementation of the paper and is recognised as being a simplification of the practical problem. Rather the focus is on demonstrating the capabilities of machine learning in field of wind energy.
Reinforcment Learning
More in-depth introductions to the paradigms of Machine Learning (ML) will be given in future blog posts but for now a brief overview of RL and the algorithm applied as part of this project (Q-Learning) is given. RL is the faction of Machine Learning that relies on the formulation of a reward signal from an agent's interaction within an environment, typically RL problems rely on the exploitation of Markov decision processes (MDPs), a framework that enables the formulation of an agent’s interaction within an environment.
Q-learning is a model-free RL algorithm which aims to learn the best policy, mapping the optmial action to take relative to a given state. Through exploration of the environment, the algorithm will iteratively update the action-value function \(Q_{\pi}(s_{t},a_{t})\) quantifying the value for all explored state-action pairs by applying the Q-learning Bellman Equation, as per Sutton and Barto (2014):
The equation shows the recursive updates made to the state-action pairs, where \({\alpha}\) is the learning rate determining the step size of updates between iterations, \({R_{t}}\) is the reward signal, \({\gamma}\) is the discount factor, determining the degree to which future reward is to be considered. In order to promote effective learning during training, it’s necessary to balance the exploration and exploitation of actions to allow for the effective mapping of action-value pairs. Hence, the actions are selected relative to an \({\epsilon}\)-greedy policy, where the action with the highest value is selected with respect to a probability of \({1-\epsilon}\) and explores randomly with a probability \({\epsilon}\).
In the context of this problem the wind turbines are the agents interacting with the FLORIS environment and in order to produce a Q-table the action space has been discretised to three possible iterations of yaw angles at each time step:
$${ action\_space =\{\alpha(\Delta\gamma) \ | \ \alpha\in \{-1, 0 ,1\}\} }$$Where \({\Delta\gamma}\) is the fixed yaw rate per time step. Noting that \({-ve}\) turbine terminations have been eliminated through the incursion of a negative reward. This provides the basis for comparison for baseline scenario which also limits turbines to positive yaw iterations. This constraint was investigated during implementation, as intuitively it would be expected that the optimised solution would alternate in wake deflection angles between turbines. This solution is found in some training runs but generally it was found to decrease the stability of the simulation opposed to forced positive yaws methodology. In order to achieve an effective yaw misalignment strategy, agents have to be able to coordinate actions with other wind turbines. The applied value function looks to maximise the current and downstream yields turbine yields, although a distinctly independent approach, it is recognised that effective optimisations can be achieved, although not necessary a global maximisation:
$${ V_{i, t} = P_{i,t} + \sum_{j\ \in \ T_{DS}} P_{j,t} }$$\({P_{i,t}}\) is the power of turbine \({i}\) at timestep \({t}\) and \({P_{j,t}}\) is the power of downstream turbines affected by the action of turbine \({i}\) encouraging each agent to balance the overall wind farm power by the effect of current turbine's action. The value function is used to calculate the reward signal, in which a slight deviation to the paper may be observed:
Setup & Environment
FLORIS is an open-source tool used for control-orientated modelling of wind farms, it can be used to model wake interactions in wind farms and provide insight into supervisory control strategies. The model has been used to produce the foundation of the steady-state environment in this project and with further amendments allowed for an inferred wake propagation component to the model, enabling the simulation of a quasi-dynamic environment. To account for temporal propagation of wakes, Taylor's frozen wake hypothesis has been applied, in which it is assumed that the wake profile propagates in space unchanged with the time delay relative to the distance and freestream wind speed. This is an over-simplification of a practical windfarm environment but helps to add further depth to the RL problem.
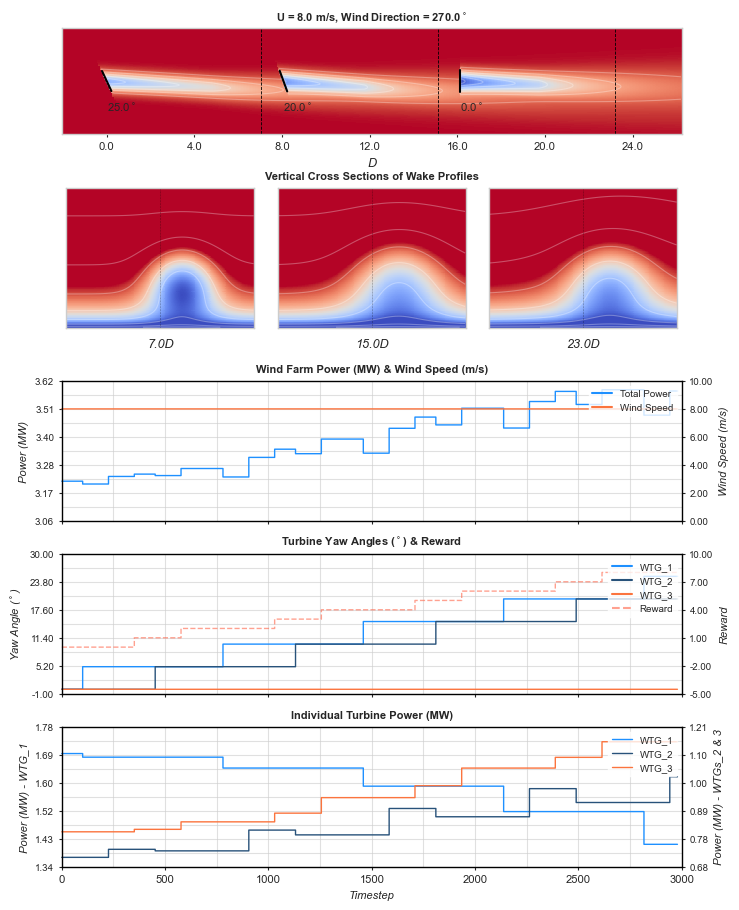
In order to optimise the turbines with a conventional Q-learning algorithm, the state space was discretised, allowing for state-values to be predicted from pre-determined yaw-angle increments, referred to as \({\Delta}{\gamma}\) through this post. As seen in figure 1 the simulated environment consists of three turbines, although a simplified layout the approach detailed can be scaled to larger layouts. In practice turbines could be clustered relative to the prevailing wind direction and wake steering optimised independently within grouped turbines.
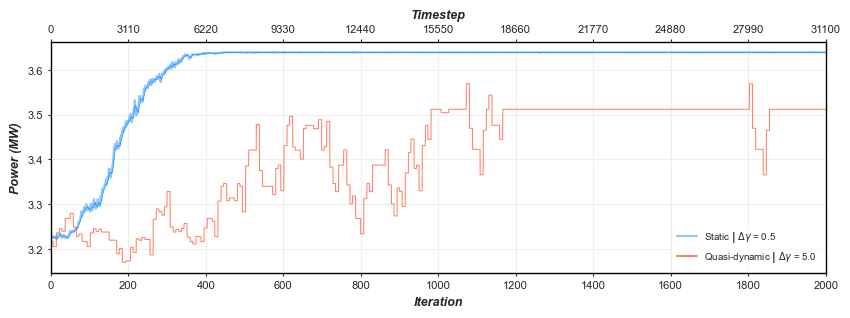
Figure 2 illustrates wind farm power output during the optimisation of the Q-Learning algorithm for both the static and quasi-dynamic environments. To illustrate the stepped progression of the dynamic environment a higher yaw rate (\({\Delta}{\gamma}\)) of 5.0 was applied during training, this helped to find an optimised solution faster, comprising on the additional runtimes observed from the wake propagation strategy. This is opposed to the static environment in which a \({\Delta}{\gamma} = 0.5\) was adopted and as can be observed results in ~3.1% uplift when compared to the quasi-dynamic environment.
Results
The animation in figure 3 illustrates the performance of the optimised dynamic model over time, showing the reduced requirement for wake steering with increasing wind speeds. An uncompressed gif file, of this animation, is available on Github. In an attempt to better highlight the propagation of wakes in time, vertical cross sections have been plotted, updating sequentially throughout the time steps to emphasise the delayed wakes, that may not be as readily apparent from the horizontal cross section. These cross sections are complemented by the further detail portrayed in the line graphs, depicting; total wind farm power, wind speed, individual turbine yaw angles, overall accumulated reward and individual turbine powers.
The animation runs greedily with respect state-values devised during the optimisation shown in figure 2, using a \({\Delta}{\gamma}=5.0\). Although greater power yields can be achieved with a smaller \({\Delta}{\gamma}\) a value of 5.0 helps to reduce animation time whilst emphasising the effects of yaw angle increments.
Conclusions + Further Work
The primary motivation of this blog post was to gain some insight and experience of implementation a RL problem. Although more practical and efficient optimisations exist for the yaw steering problem, this fairly rudimental RL implementation highlights the opportunity for what is still perceived as still very novel control methodologies. Through discretizing the state space, Q-learning has shown to yield effective results, surpassing improvements proposed by traditional optimisation techniques. Applying other RL algorithms, including variants of Q-Learning such as Deep Q Networks (DQNs), could help move away from a discretized state space and bring a higher order of practicality to the problem, catering for the variability in yaw rates and allow irregular optimised yaw angles not confined by the binned states.
Resources
- https://www.nrel.gov/docs/fy20osti/75889.pdf
- https://github.com/emerrf/gym-wind-turbine
- https://web.stanford.edu/class/psych209/Readings/SuttonBartoIPRLBook2ndEd.pdf
Code
# Code implementation of NREL coference paper: https://www.nrel.gov/docs/fy20osti/75889.pdf
# Richard Findlay 20/03/2021
import floris.tools as wfct
import gym
from gym import spaces
import multiprocessing as mp
import numpy as np
import os
import pickle
from qdynplots import simulation_graphs
class floris_env(gym.Env):
def __init__(self, env_settings):
# instaniate turbine layout parameters
self.n_row = env_settings['number_of_turbines_y']
self.n_col = env_settings['number_of_turbines_x']
self.x_space = env_settings['x_spacing']
self.y_space = env_settings['y_spacing']
self.run_type = env_settings['run_type']
# intialise floris environment from json
file_dir = os.path.dirname(os.path.abspath(__file__))
self.fi = wfct.floris_interface.FlorisInterface(
os.path.join(file_dir, "./input_params.json")
)
# get turbine diameter
self.D = self.fi.floris.farm.turbines[0].rotor_diameter
# define layout
self.layout_x = []
self.layout_y = []
for i in range(self.n_row):
for j in range(self.n_col):
self.layout_x.append(j * self.x_space * self.D)
self.layout_y.append(i * self.y_space * self.D)
#instialise Floris environment
self.floris = self.intialise_floris()
# establish boundaries to environment
min_max_limits = np.array([
[0.0, 30.0], # wind speed [m/s]
[0.0, 359.0], # wind direction (degrees)
[0.0, np.inf], # total wind farm power
[0, 80.0], # yaw angle
[0.0, np.inf] # reward function
])
self.observation_space = spaces.Box(
low=min_max_limits[:,0],
high=min_max_limits[:,1])
# declare action space
self.action_space = spaces.Discrete(3)
# rate of yaw change per time step
self.delta_gamma = 5.0
# number of wtgs
self.agents = 3
# no yaw angle change
self.no_action = 1
# some intial parameters
self.i = 0 # timestep
self.ep = 0 # intialise episode ref
self.prev_reward = None
self.game_over = False
# decalre array for turbine yaws to be stored
self.int_outer_wake_angle = np.zeros((self.agents))
self.intial_wake_angles = np.zeros((self.agents))
# turbine yaw arrays, store previous yaws to implied dynamic env
self.turbine_yaws = np.zeros((self.agents))
self.pre_turbine_yaws = np.zeros((self.agents))
# store observations between timesteps
self.turbine_observations = {'WT' + str(wtg): 0 for wtg in range(self.agents)}
self.turbine_refs = list(self.turbine_observations.keys())
# Previous rewards per turbine
self.previous_rewards = {'WT' + str(wtg): None for wtg in range(self.agents)}
# calculate wake delay times relative to each turbine and WS
sep_distances = {}
outer_wake_dis = {}
self.wake_prop_times = {}
self.out_wake_prop_times = {}
x_coords, y_coords = self.fi.get_turbine_layout()
# calculate the wake propagation times
for i in range(len(x_coords)):
x_ref, y_ref = x_coords[i], y_coords[i]
#calculate distances broadcasting from ref to all turbine arrays - dictionary for each turbine
sep_distances['WT_%s' %i] = np.sqrt((x_coords - x_ref)**2 + (y_coords - y_ref)**2)
# outer wake prop time
average_distances = np.sum(sep_distances['WT_%s' %i]) / (self.agents)
outer_wake_dis['WT_%s' %i] = sep_distances['WT_%s' %i][-1] + average_distances
# get froozen wake propopgation times
for w in env_settings['wind_speeds']:
self.wake_prop_times['WT%s_WS_%sm/s' %(i, w)] = sep_distances['WT_%s' %i] // w # may need to make this instance of class
self.wake_prop_times['WT%s_WS_%sm/s' %(i, w)][:i] = 0 # make upstream turbines 0
# calculate outer wake prop time
self.out_wake_prop_times['WT%s_WS_%sm/s' %(i, w)] = outer_wake_dis['WT_%s' %i] // w
# array for saving wake delay times
self.wake_delays = np.zeros((self.agents))
self.out_wake_delays = -1.0 # < 0 to statisfy intial statement
self.out_index = 0
#previous wind speed
self.prev_ws = None
# set all turbines as unlocked (false)
self.locked_turbines = np.zeros((self.agents), dtype=bool)
# initialise turbine powers:
self.turbine_pwrs = np.zeros((self.agents))
# set intial previous previous turbine ref
self.prev_turbine = None
# vars for animation rendering
self.plotter_data = mp.Queue()
self.is_plotter_active = False
# int to follow wake propogation time for external ref in vis
self.outer_wake_time = 0
# set simulation to render
if env_settings['render']:
self.render()
# store intial powers
self.fi.calculate_wake()
self.baseline_wake_pwr = self.fi.get_turbine_power()
def reintialise_floris(self, wind_speed):
self.floris.reinitialize_flow_field(wind_speed = wind_speed)
def intialise_floris(self, wind_speed=8.0):
WD = 270 # constant and only WD considered in this example
# intialise the flow field in floris
self.fi.reinitialize_flow_field(
layout_array = (self.layout_x, self.layout_y), wind_direction=WD, wind_speed=wind_speed
)
return self.fi
def step(self, action, idx, itnial_obs, ws):
# refresh wake delay times for specific turbine
if (self.prev_turbine != idx):
if self.run_type == 'dynamic':
self.i += 1 # increase timestep
# intialise wake delays
self.wake_delays = np.copy(self.wake_prop_times['WT%s_WS_%sm/s' %(idx, ws)])
# initlase 'settle' time
self.settle = 100 # timesteps
else: # env_settings['run_type'] == 'dynamic'
self.wake_delays = np.zeros_like(self.wake_prop_times['WT%s_WS_%sm/s' %(idx, ws)])
self.settle = 0
# make copy of intial turbine powers
self.intial_powers = np.copy(self.baseline_wake_pwr)
# store intial/previous wakes before current turbine move
self.intial_wake_angles = np.copy(self.turbine_yaws)
# refresh outer wake delay for vertical cross visualisation
if self.out_wake_delays <= -1 and (self.prev_turbine != idx):
self.out_wake_delays = np.copy(self.out_wake_prop_times['WT%s_WS_%sm/s' %(self.out_index, ws)])
self.int_outer_wake_angle = np.copy(self.intial_wake_angles)
if self.out_index <= 1:
self.out_index += 1
else:
self.out_index = 0
# update intial previous wind speed
if self.prev_ws is None:
self.prev_ws = ws
# add a time delay allowing actions to settle between different turbine actions
if self.settle != 0:
reward = 0
done = False
self.i += 1
self.prev_turbine = idx
if self.i > self.settle :
self.out_wake_delays -= 1
# return info for optmisation algorithms
info = {
'locked_turbines': self.locked_turbines,
'wake_delays': self.wake_delays,
'timestep': self.i
}
plotter_data_ = {
'ts': self.i,
'ws': self.observation[0],
'wd': self.observation[1],
'turb_pwr': tuple(self.baseline_wake_pwr),
'tot_farm_pwr': self.observation[2],
'turb_yaw': self.observation[3],
'windfarm_yaws': tuple(self.turbine_yaws),
'prev_windfarm_yaws': tuple(self.pre_turbine_yaws),
'intial_windfarm_yaws': tuple(self.intial_wake_angles),
'locked_turb': tuple(self.locked_turbines),
'out_wake_delays': self.outer_wake_time,
'intial_outer_wake':tuple(self.int_outer_wake_angle),
'turb_ref': idx,
'reward': 0,
'floris': self.floris
}
# pass plotting data only if render is active
if self.is_plotter_active:
self.plotter_data.put(plotter_data_)
self.settle -= 1
return self.observation, reward, done, info
#end simulation if observation of action out of bounds
self.game_over = not self.observation_space.contains(self.observation)
# turbine yaw and reward updates only if all turbines
if np.all(self.locked_turbines == False):
# take action if turbines are unlocked
self.turbine_yaws[idx] += ((action - 1) * self.delta_gamma)
# calcaulte updated wakes i.e. turbine powers
self.floris.calculate_wake(yaw_angles=self.turbine_yaws)
self.turbine_pwrs = self.floris.get_turbine_power()
# if no turbines are yet locked immediately update power of current turbine
if self.baseline_wake_pwr[idx] != self.turbine_pwrs[idx]:
self.baseline_wake_pwr[idx] = self.turbine_pwrs[idx]
self.i -= 1 # instantenous change
# get power differences from updated action
wake_diff = np.array(self.baseline_wake_pwr) - np.array(self.turbine_pwrs)
# lock turbines with power change (other than the the one that underwent action)
self.locked_turbines = np.array(wake_diff, dtype=bool)
# make wait inducing turbine unlocked
self.locked_turbines[idx] = False
# check wake delays, decide if to update power of that turbine
for t, times in enumerate(self.wake_delays):
if times == 0 and self.baseline_wake_pwr[t] != self.turbine_pwrs[t]:
self.baseline_wake_pwr[t] = self.turbine_pwrs[t]
self.locked_turbines[t] = False
self.i -= 1
else:
continue
# update observations for step
self.observation = np.array([ws, 270.0, np.sum(self.baseline_wake_pwr), self.turbine_yaws[idx], np.sum(self.baseline_wake_pwr[idx:])])
# update current and previous yaws and powers
(_, _, _, Y, P) = self.observation
(_, _, _, prev_Y, prev_P) = np.array([self.prev_ws, 270.0, np.sum(self.intial_powers), self.turbine_yaws[idx], np.sum(self.intial_powers[idx:])])
# update reward only if all turbines are unlocked
if np.all(self.locked_turbines == False):
P_change = P - prev_P
else:
P_change = 0
# reward signals
if P_change > 0:
reward = 1.0
elif abs(P_change) == 0:
reward = 0.0
elif P_change < 0:
reward = -1.0
# deter algo from choosing -ve yaws, creates instability
if self.turbine_yaws[idx] < 0:
reward -= 10
done = False
if self.game_over:
reward = -10.0
done = True
self.turbine_yaws[idx] = 0
# store some previous vars
self.previous_rewards[self.turbine_refs[idx]] = reward
self.prev_reward = reward
self.prev_action = action
self.prev_turbine = idx
if self.prev_ws != ws:
self.prev_ws = ws
# update timestep
self.i += 1
if np.all(self.wake_delays == 0) or np.all(self.locked_turbines == False):
done = True
# store lagged wake moves for visual
for turbine in range(self.agents):
if self.out_wake_delays == 0:
self.pre_turbine_yaws[-1] = self.turbine_yaws[-1]
elif turbine <= 1 and self.locked_turbines[turbine+1] == False:
self.pre_turbine_yaws[turbine] = self.turbine_yaws[turbine]
else:
continue
# update wake delay times & clip -ve to zeros
self.wake_delays[self.wake_delays > 0] -= 1
self.out_wake_delays -= 1
self.outer_wake_time = np.copy(self.out_wake_delays)
# info for solvers
info = {
'locked_turbines': self.locked_turbines,
'wake_delays': self.wake_delays,
'timestep': self.i
}
# store data for graphs
plotter_data_ = {
'ts': self.i,
'ws': self.observation[0],
'wd': self.observation[1],
'turb_pwr': tuple(self.baseline_wake_pwr),
'tot_farm_pwr': self.observation[2],
'turb_yaw': self.observation[3],
'windfarm_yaws': tuple(self.turbine_yaws),
'prev_windfarm_yaws': tuple(self.pre_turbine_yaws),
'intial_windfarm_yaws': tuple(self.intial_wake_angles),
'locked_turb': tuple(self.locked_turbines),
'out_wake_delays': self.outer_wake_time ,
'intial_outer_wake':tuple(self.int_outer_wake_angle),
'turb_ref': idx,
'reward': reward,
'floris': self.floris
}
if self.is_plotter_active:
self.plotter_data.put(plotter_data_)
return self.observation, reward, done, info
def reset(self, idx, ws):
self.ep += 1
self.prev_action = None
self.game_over = False
self.wake_delays = np.zeros((self.agents))
self.observation = np.array([ws, 270.0, np.sum(self.baseline_wake_pwr), self.turbine_yaws[idx], np.sum(self.baseline_wake_pwr[idx:])])
plotter_data_ = {
'ts': self.i,
'ws': self.observation[0],
'wd': self.observation[1],
'turb_pwr': tuple(self.baseline_wake_pwr),
'tot_farm_pwr': self.observation[2],
'turb_yaw': self.observation[3],
'windfarm_yaws': tuple(self.turbine_yaws),
'prev_windfarm_yaws': tuple(self.pre_turbine_yaws),
'intial_windfarm_yaws': tuple(self.intial_wake_angles),
'locked_turb': tuple(self.locked_turbines),
'out_wake_delays': self.outer_wake_time,
'intial_outer_wake': tuple(self.int_outer_wake_angle),
'turb_ref': idx,
'reward': 0,
'floris': self.floris
}
if self.is_plotter_active:
self.plotter_data.put(plotter_data_)
return self.observation
def render(self):
if (self.run_type == 'static'):
print('Rendering is only available in dynamic runtime')
raise NotImplementedError
#some extra vars to pass to plots
plot_vars = {'diameter': self.D,
'agents': self.agents,
'x_spacing': self.x_space}
if not self.is_plotter_active:
self.is_plotter_active = True
self.p = mp.Process(target=simulation_graphs, args=(self.plotter_data, plot_vars,))
self.p.start()
# time.sleep(3)
# self.p.join()
elif self.is_plotter_active:
# allow delay for mp to finalise
time.sleep(3)
# Richard Findlay 20/03/2021
import matplotlib.pyplot as plt
import numpy as np
import os
import pickle
from environment import floris_env
import warnings
warnings.filterwarnings("ignore")
# define bins for state spaces
ws_space = np.linspace(1, 25, 25)
wd_space = np.linspace(0, 359, 36)
yaw_space = np.linspace(0, 89, int(90 / 1.0)) # update depending on yaw rate
# function to discretize state space
def discete_state(observation, idx):
ws, wd, _, yaw, _ = observation
ws_bin = np.digitize(ws, ws_space)
wd_bin = np.digitize(wd, wd_space)
yaw_bin = np.digitize(yaw, yaw_space)
return (ws_bin, wd_bin, yaw_bin)
# function to get best action from q-table
def max_action(Q, state, actions=[0,1,2]):
values = np.array([Q[state, a] for a in actions])
action = np.argmax(values)
return action
# function to save Q-learning table
def save_table(var, filename):
with open(filename, 'wb') as f:
pickle.dump(var ,f)
# function to load Q-Learning table
def load_table(filename):
with open(filename, 'rb') as f:
data = pickle.load(f)
return data
def q_learning():
# declare array of wind speeds
all_ws = [8.0]
# declare environment dictionary
env_settings = {
'agents': 3,
'wind_speeds': all_ws,
'number_of_turbines_x': 3,
'number_of_turbines_y': 1,
'x_spacing': 8,
'y_spacing': 1,
'run_type':'dynamic', # 'dynamic' or 'static'
'render': True
}
env = floris_env(env_settings)
alpha = 0.01
gamma = 1.0
epsilon_decay = 0.995
epsilon_min = 0.01
episodes= 1000
states = []
for ws in range(len(ws_space)):
for wd in range(len(wd_space)):
for yaw in range(len(yaw_space)):
states.append((ws, wd, yaw))
# dictionary in dictionary for multi-agent environment
Q_agents = {}
Q = {}
for agent in range(env_settings['agents']):
Q_agents['WT%s' %agent]= {}
for state in states:
for action in [0,1,2]:
Q_agents['WT%s' %agent][state, action] = 0.0
tot_rew = np.zeros((episodes))
# some lists used in training or testing
powers = []
# yaw increment / rate
env.delta_gamma = 0.5
# check for existing q-learning table
fname = 'q_learning_table.pkl'
if not os.path.isfile(fname):
for ws in all_ws: # find optimal solution for all desired wind speeds
epsilon = 1.0
# intialise baseline floris model
env.reintialise_floris(ws)
for ep in range(episodes):
epi_rew = 0
for idx, agent in enumerate(Q_agents.keys()):
done = False
obs = env.reset(idx, ws)
state = discete_state(obs, idx)
# take action for first turbine iteration, remains the same until trubine changes
action = np.random.choice([0,1,2]) if np.random.random() < epsilon else max_action(Q_agents[agent], state)
while not done:
obs_, reward, done, info = env.step(action, idx, obs, ws)
state_ = discete_state(obs_, idx)
action_ = max_action(Q_agents[agent], state_)
if np.all(info['locked_turbines'] == False):
Q_agents[agent][state, action] += alpha*(reward + gamma*Q_agents[agent][state_, action_] - Q_agents[agent][state, action])
epi_rew += reward
state = state_
if idx == (env_settings['agents'] - 1):
powers.append(obs_[2])
tot_rew[ep] += epi_rew
print("Agent:{}\n Episode:{}\n Reward:{}\n Epsilon:{}".format(agent, ep, reward, epsilon))
epsilon = epsilon - 2/episodes if epsilon > 0.01 else 0.01
# epsilon *= epsilon_decay
# epsilon = max(epsilon, epsilon_min)
# save q-learning table
save_table(Q_agents, fname)
mean_rewards = np.zeros(episodes)
for t in range(episodes):
mean_rewards[t] = np.mean(tot_rew[max(0, t-50):(t+1)])
# plt.plot(mean_rewards)
# plt.show()
# plt.plot(timestep, powers)
# plt.show()
# plt.plot(powers)
# plt.show()
else:
# number of test episodes
test_episodes = [10]
# load trained Q-learning table
print('loading data...')
Q_agents = load_table(fname)
for idx, ws in enumerate(all_ws):
env.reintialise_floris(ws)
# test best q-learning tables and plot best result
for ep in range(test_episodes[idx]):
print(ep)
epi_rew = 0
for idx, agent in enumerate(Q_agents.keys()):
done = False
obs = env.reset(idx, ws)
state = discete_state(obs, idx)
# take action for first turbine iteration, remains the same until trubine changes
action = max_action(Q_agents[agent], state)
while not done:
obs_, reward, done, info = env.step(action, idx, obs, ws)
state_ = discete_state(obs_, idx)
action_ = max_action(Q_agents[agent], state_)
state = state_
if __name__ == '__main__':
q_learning()
# Richard Findlay 20/03/2021
import floris.tools as wfct
import numpy as np
import os
import pickle
import matplotlib
import matplotlib.pyplot as plt
from matplotlib.lines import Line2D
from matplotlib.animation import FuncAnimation
import matplotlib.animation as animation
import matplotlib.gridspec as gridspec
from matplotlib import ticker as mtick
from matplotlib.ticker import FormatStrFormatter
import multiprocessing as mp
from multiprocessing import Process, Manager
def simulation_graphs(graph_data, plot_vars):
plt.style.use(['seaborn-whitegrid'])
plt.ion() #activate interactive plot
# store some pertinent vars
diameter = plot_vars['diameter']
agents = plot_vars['agents']
x_spacing = plot_vars['x_spacing']
# Declare lists for graph vars
time_all = []
windfarm_power_all = []
reward_all =[]
ws_all = []
first_turbine_powers_all = []
# some vars relative to each agent, hence use dictionary of lists
# declare dictionaries
turbine_yaws_all = {}
turbine_powers_all = {}
for agent in range(agents):
turbine_yaws_all['turbine_%s' %agent] = []
for index in range(1,3):
turbine_powers_all['turbine_%s' %index] = []
# figure setup
fig = plt.figure(figsize=(8, 12), constrained_layout=False)
gs = gridspec.GridSpec(ncols=50, nrows=230)
# subplot layouts
row_start = 43
col_width = 50
trb_plan = fig.add_subplot(gs[0:row_start, 0:col_width])
# create wake profile sub plots, depending on number of agents
wake_profiles = {}
cross_sections = {}
row_spacing = row_start
col_spacing = 0
for idx in range(1, agents+1):
# create dictionary of wake profiles
wake_profiles['wake_profile_%s' %idx] = fig.add_subplot(gs[(row_spacing + 5):(row_spacing + 40), (col_spacing + (idx-1)):(col_spacing + (idx-1) + 16)])
wake_profiles['wake_profile_%s' %idx].set_facecolor('#b40826') # compensate for reduce plot size at higher WS
# update col_spcaing to a fixed third of the window
col_spacing = col_spacing + 16
# for each for of three increase row_spacing
if (idx * agents) == 0:
row_spacing += 30
col_spacing = 0
# increase buffer between graphs
row_spacing += 8
# plot line graphs for power, reward etc.
wf_pwr = fig.add_subplot(gs[row_spacing+45:row_spacing+80, 0:50])
trb_yaws = fig.add_subplot(gs[row_spacing+88:row_spacing+123, 0:50])
trb_pwrs = fig.add_subplot(gs[row_spacing+131:row_spacing+166, 0:50])
# remove borders from
# fig.subplots_adjust(left=0, bottom=0, right=1, top=1, wspace=None, hspace=None)
# function to update existing y-labels from watts to mega-watts
def pwrfmt(x, pos):
s = '{:0.2f}'.format(x / 1000000.0) # watts to MW
return s
yfmt = mtick.FuncFormatter(pwrfmt)
#######_First_Line_Plot_#######################################################################################
# Left Axis -> Wind Farm power | Right Axis -> Wind Speed
wf_pwr.grid(True, alpha=0.6, which="both")
wf_pwr_line, = wf_pwr.plot([],[], color='dodgerblue', lw="1.0", label='Total Power', zorder=2, clip_on=False)
wf_pwr.set_title('Wind Farm Power (MW) & Wind Speed (m/s)', fontsize=8, fontweight='bold')
wf_pwr.set_xticklabels([])
wf_pwr.tick_params(axis='y', labelsize= 7)
wf_pwr.set_ylabel('Power (MW)', fontsize=8, style='italic')
# intialise plot for second axis
sec_ax_wfpwr = wf_pwr.twinx()
sec_ax_wfpwr.grid(False)
wf_pwr_line_sec, = sec_ax_wfpwr.plot([],[], color='#fb743e', lw="1.0", label='Wind Speed', clip_on=False, zorder=2)
sec_ax_wfpwr.tick_params(axis='y', labelsize= 7)
sec_ax_wfpwr.set_ylabel('Wind Speed (m/s)', fontsize=8, style='italic')
# clean up splines - both axes
wf_pwr.spines['top'].set_visible(False)
wf_pwr.spines['bottom'].set_visible(False)
wf_pwr.spines['left'].set_visible(False)
wf_pwr.spines['right'].set_visible(False)
sec_ax_wfpwr.spines['top'].set_color('black')
sec_ax_wfpwr.spines['bottom'].set_color('black')
sec_ax_wfpwr.spines['left'].set_color('black')
sec_ax_wfpwr.spines['right'].set_color('black')
# line-up gridlines
wf_pwr.yaxis.set_major_locator(mtick.LinearLocator(6))
sec_ax_wfpwr.yaxis.set_major_locator(mtick.LinearLocator(6))
# add minor ticks and locate
wf_pwr.minorticks_on()
wf_pwr.xaxis.set_minor_locator(matplotlib.ticker.AutoMinorLocator(2))
wf_pwr.yaxis.set_minor_locator(matplotlib.ticker.AutoMinorLocator(2))
# add tick marks
wf_pwr.tick_params(direction="out", length=2.0)
sec_ax_wfpwr.tick_params(direction="out", length=2.0)
# axis limits
wf_pwr.set_ylim([3055949, 3377628])
wf_pwr.set_xlim([0, 1500])
sec_ax_wfpwr.set_ylim([0, 10])
# convert watts to mega-watts
wf_pwr.yaxis.set_major_formatter(yfmt)
sec_ax_wfpwr.yaxis.set_major_formatter(FormatStrFormatter('%.2f'))
# plot single legend for multiple axes
handle1, label1 = wf_pwr.get_legend_handles_labels()
handle2, label2 = sec_ax_wfpwr.get_legend_handles_labels()
leg = wf_pwr.legend(handle1+handle2, label1+label2, loc="upper right", fontsize=7, frameon=True)
leg.set_zorder(5)
# line width for ledgend
for line in leg.get_lines():
line.set_linewidth(1.5)
# legend background and frame color
frame = leg.get_frame()
frame.set_facecolor('white')
frame.set_edgecolor('white')
#######_Second_Line_Plot_#######################################################################################
# Left Axis -> Turbine Yaws | Right Axis -> Reward
trb_yaws.grid(True, alpha=0.6, which="both")
# plot first axis
color = ['dodgerblue', '#28527a', '#fb743e']
turbine_refs = ['WTG_1', 'WTG_2', 'WTG_3']
turb_yaw_lines = []
for agent in range(agents):
trb_yaw_line, = trb_yaws.plot([],[], color=color[agent], lw="1.0", label=turbine_refs[agent], zorder=2, clip_on=False)
turb_yaw_lines.append(trb_yaw_line)
trb_yaws.set_title('Turbine Yaw Angles ($^\circ$) & Reward', fontsize=8, fontweight='bold', zorder=10)
trb_yaws.set_xticklabels([])
trb_yaws.tick_params(axis='y', labelsize= 7)
trb_yaws.set_ylabel('Yaw Angle ($^\circ$)', fontsize=8, style='italic')
# intialise plot for second axis
sec_ax_trb_yaws = trb_yaws.twinx()
sec_ax_trb_yaws.grid(False)
trb_yaws_sec, = sec_ax_trb_yaws.plot([],[], color='tomato', lw="1.0", label='Reward', zorder=2, clip_on=False, alpha=0.6, linestyle='dashed')
sec_ax_trb_yaws.tick_params(axis='y', labelsize=7)
sec_ax_trb_yaws.set_ylabel('Reward', fontsize=8, style='italic')
# clean up splines - both axes
trb_yaws.spines['top'].set_visible(False)
trb_yaws.spines['bottom'].set_visible(False)
trb_yaws.spines['left'].set_visible(False)
trb_yaws.spines['right'].set_visible(False)
sec_ax_trb_yaws.spines['top'].set_color('black')
sec_ax_trb_yaws.spines['bottom'].set_color('black')
sec_ax_trb_yaws.spines['left'].set_color('black')
sec_ax_trb_yaws.spines['right'].set_color('black')
# line-up gridlines
trb_yaws.yaxis.set_major_locator(mtick.LinearLocator(6))
sec_ax_trb_yaws.yaxis.set_major_locator(mtick.LinearLocator(6))
# add minor ticks and locate
trb_yaws.tick_params(direction="out", length=2.0)
sec_ax_trb_yaws.tick_params(direction="out", length=2.0)
trb_yaws.minorticks_on()
trb_yaws.xaxis.set_minor_locator(matplotlib.ticker.AutoMinorLocator(2))
trb_yaws.yaxis.set_minor_locator(matplotlib.ticker.AutoMinorLocator(2))
# axis limits
trb_yaws.set_ylim([-1, 10])
trb_yaws.set_xlim([0, 1500])
sec_ax_trb_yaws.set_ylim([-5, 5])
# format labels
trb_yaws.yaxis.set_major_formatter(FormatStrFormatter('%.2f'))
sec_ax_trb_yaws.yaxis.set_major_formatter(FormatStrFormatter('%.2f'))
# plot single legend for multiple axes
handle1, label1 = trb_yaws.get_legend_handles_labels()
handle2, label2 = sec_ax_trb_yaws.get_legend_handles_labels()
leg = sec_ax_trb_yaws.legend(handle1+handle2, label1+label2, loc="upper right", fontsize=7, frameon=True)
leg.set_zorder(5)
# line width for ledgend
for line in leg.get_lines():
line.set_linewidth(1.5)
# legend background and frame color
frame = leg.get_frame()
frame.set_facecolor('white')
frame.set_edgecolor('white')
#######_Third_Line_Plot_#######################################################################################
# Left Axis -> Individual Turbine Powers (WTG1) | Right Axis -> Individual Turbine Powers (WTG2 & 3)
trb_pwrs.grid(True, alpha=0.6, which="both")
trb_pwrs_line, = trb_pwrs.plot([],[], color='dodgerblue', lw="1.0", label='WTG_1', zorder=2, clip_on=False)
trb_pwrs.set_title('Individual Turbine Power (MW)', fontsize=8, fontweight='bold')
trb_pwrs.set_xlabel('Timestep', fontsize=8, style='italic')
trb_pwrs.tick_params(axis='y', labelsize= 7)
trb_pwrs.tick_params(axis='x', labelsize= 8)
trb_pwrs.set_ylabel('Power (MW) - WTG_1', fontsize=8, style='italic')
# instaniate and plot second axis
sec_ax_trb_pwrs = trb_pwrs.twinx()
sec_ax_trb_pwrs.grid(False)
color = ['#28527a', '#fb743e']
turbine_refs = ['WTG_2', 'WTG_3']
sec_trb_pwrs_lines = []
for agent in range(agents-1):
trb_pwrs_sec, = sec_ax_trb_pwrs.plot([],[], color=color[agent], lw="1.0", label=turbine_refs[agent], zorder=2, clip_on=False)
sec_trb_pwrs_lines.append(trb_pwrs_sec)
# general format of second access
sec_ax_trb_pwrs.tick_params(axis='y', labelsize= 7)
sec_ax_trb_pwrs.set_ylabel('Power (MW) - WTGs_2 & 3', fontsize=8, style='italic', zorder=10)
# clean up splines
trb_pwrs.spines['top'].set_visible(False)
trb_pwrs.spines['bottom'].set_visible(False)
trb_pwrs.spines['left'].set_visible(False)
trb_pwrs.spines['right'].set_visible(False)
sec_ax_trb_pwrs.spines['top'].set_color('black')
sec_ax_trb_pwrs.spines['bottom'].set_color('black')
sec_ax_trb_pwrs.spines['left'].set_color('black')
sec_ax_trb_pwrs.spines['right'].set_color('black')
# line-up gridlines
trb_pwrs.yaxis.set_major_locator(mtick.LinearLocator(6))
sec_ax_trb_pwrs.yaxis.set_major_locator(mtick.LinearLocator(6))
# add minor ticks and locate
trb_pwrs.tick_params(direction="out", length=2.0)
sec_ax_trb_pwrs.tick_params(direction="out", length=2.0)
trb_pwrs.minorticks_on()
trb_pwrs.xaxis.set_minor_locator(matplotlib.ticker.AutoMinorLocator(2))
trb_pwrs.yaxis.set_minor_locator(matplotlib.ticker.AutoMinorLocator(2))
# axis limits
trb_pwrs.set_ylim([1542785, 1712322])
sec_ax_trb_pwrs.set_ylim([676376, 849917])
trb_pwrs.set_xlim([0, 1500])
# convert watts to mega-watts
trb_pwrs.yaxis.set_major_formatter(yfmt)
sec_ax_trb_pwrs.yaxis.set_major_formatter(yfmt)
# plot single legend for multiple axes
handle1, label1 = trb_pwrs.get_legend_handles_labels()
handle2, label2 = sec_ax_trb_pwrs.get_legend_handles_labels()
leg = sec_ax_trb_pwrs.legend(handle1+handle2, label1+label2, loc="upper right", fontsize=7, frameon=True)
leg.set_zorder(5)
# line width for ledgend
for line in leg.get_lines():
line.set_linewidth(1.5)
# legend background and frame color
frame = leg.get_frame()
frame.set_facecolor('white')
frame.set_edgecolor('white')
# define update function for animation
def update(i):
# get data from queue
data = graph_data.get()
# get current floris obj from queue
fi = data['floris']
# collate data from queue
time_all.append(data['ts'])
ws_all.append(data['ws'])
windfarm_power_all.append(data['tot_farm_pwr'])
# get turbine yaw data
current_wtg_ref = data['turb_ref']
for agent in range(agents):
if current_wtg_ref == agent:
turbine_yaws_all['turbine_%s' %agent].append(data['turb_yaw'])
elif not turbine_yaws_all['turbine_%s' %agent]:
turbine_yaws_all['turbine_%s' %agent].append(0)
else:
turbine_yaws_all['turbine_%s' %agent].append(turbine_yaws_all['turbine_%s' %agent][-1])
# turbine power for primary axis
first_turbine_powers_all.append(data['turb_pwr'][0])
# turbine powers for secondary axis
for agent in range(1,3):
turbine_powers_all['turbine_%s' %agent].append(data['turb_pwr'][agent])
# cumaltive reward
if len(reward_all) > 0:
cumlative_reward = reward_all[-1] + data['reward']
else:
cumlative_reward = 0
reward_all.append(cumlative_reward)
# get reference for x-axis scales
_ , xlim = trb_yaws.get_xlim()
if data['ts'] >= xlim:
# change x-axis range when data out of range
wf_pwr.set_xlim(0, xlim * 2)
wf_pwr.figure.canvas.draw()
trb_yaws.set_xlim(0, xlim * 2)
trb_yaws.figure.canvas.draw()
trb_pwrs.set_xlim(0, xlim * 2)
trb_pwrs.figure.canvas.draw()
# First line graph re-scaling (left axis -> wind farm power)
ylimMin_PWR, ylimMax_PWR = wf_pwr.get_ylim()
if data['tot_farm_pwr'] >= (ylimMax_PWR * 0.99):
wf_pwr.set_ylim(ylimMin_PWR, data['tot_farm_pwr'] + (0.01*data['tot_farm_pwr']))
elif data['tot_farm_pwr'] <= ylimMin_PWR:
wf_pwr.set_ylim((data['tot_farm_pwr'] - (0.01*data['tot_farm_pwr'])), ylimMax_PWR)
# First line graph re-scaling (right axis -> wind speed)
ylimMin_WS, ylimMax_WS = sec_ax_wfpwr.get_ylim()
if data['ws'] >= (ylimMax_WS * 0.99):
sec_ax_wfpwr.set_ylim(ylimMin_WS, ylimMax_WS*2)
# Second line graph re-scaling (left axis -> turbine yaws)
ylimMin_turbYAW, ylimMax_turbYAW = trb_yaws.get_ylim()
if data['turb_yaw'] >= (ylimMax_turbYAW * 0.99):
trb_yaws.set_ylim(ylimMin_turbYAW, ylimMax_turbYAW+10)
# Second line graph re-scaling (right axis -> reward)
ylimMin_REW, ylimMax_REW = sec_ax_trb_yaws.get_ylim()
if cumlative_reward >= (ylimMax_REW * 0.99):
sec_ax_trb_yaws.set_ylim(ylimMin_REW, ylimMax_REW+5)
elif cumlative_reward <= (ylimMin_REW * 1.01):
sec_ax_trb_yaws.set_ylim(ylimMin_REW-5, ylimMax_REW)
# Third line graph re-scaling (left axis -> turbine 1 power)
ylimMin_turbPWR, ylimMax_turbPWR = trb_pwrs.get_ylim()
if data['turb_pwr'][0] >= (ylimMax_turbPWR * 0.99):
trb_pwrs.set_ylim(ylimMin_turbPWR, data['turb_pwr'][0] + (0.07 * data['turb_pwr'][0]))
elif data['turb_pwr'][0] <= (ylimMin_turbPWR):
trb_pwrs.set_ylim(data['turb_pwr'][0] - (0.07 * data['turb_pwr'][0]), ylimMax_turbPWR)
# Third line graph re-scaling (right axis -> turbine 2 & 3 power)
ylimMin_turbPWR, ylimMax_turbPWR = sec_ax_trb_pwrs.get_ylim()
if (data['turb_pwr'][1] >= ylimMax_turbPWR *0.99) or (data['turb_pwr'][2] >= ylimMax_turbPWR *0.99):
max_val = np.max(data['turb_pwr'][1:])
sec_ax_trb_pwrs.set_ylim(ylimMin_turbPWR, max_val + (0.05 * max_val))
elif (data['turb_pwr'][1] <= ylimMin_turbPWR*1.01) or (data['turb_pwr'][2] <= ylimMin_turbPWR*1.01):
min_val = np.max(data['turb_pwr'][1:])
sec_ax_trb_pwrs.set_ylim(min_val + (0.07 * min_val), ylimMax_turbPWR)
# clear previous cross sectional plots
trb_plan.cla()
for idx in range(1, agents+1):
wake_profiles['wake_profile_%s' %idx].cla()
# Update plan view cross section
wake_calcs = fi.calculate_wake(yaw_angles=list(data['windfarm_yaws'])) # updates flow profile
# Plot horizontal profile and turbine yaws
hor_plane = fi.get_hor_plane(height=fi.floris.farm.turbines[0].hub_height, y_bounds=(-400,400), x_resolution=400, y_resolution=400)
wfct.visualization.visualize_cut_plane(hor_plane, ax=trb_plan)
wfct.visualization.plot_turbines(
ax=trb_plan,
layout_x=fi.layout_x,
layout_y=fi.layout_y,
yaw_angles=list(data['windfarm_yaws']),
D=diameter
)
# Add yaw labels
for idx, yaw in enumerate(list(data['windfarm_yaws'])):
trb_plan.text((x_spacing) * (idx) * diameter, -175, "{}$^\circ$".format(yaw), fontsize=8)
# apply some formatting
trb_plan.set_title("U = {} m/s, Wind Direction = {}$^\circ$" .format(data['ws'], data['wd']), fontsize=8, fontweight='bold')
trb_plan.set_xticklabels(np.arange(-(x_spacing/2),100*x_spacing, (x_spacing/2)), fontsize=8)
trb_plan.set_xlabel('D', fontsize=9, style='italic')
trb_plan.set_yticklabels([])
trb_plan.set_yticks([])
trb_plan.tick_params(direction="out", length=2.0)
trb_plan.set_ylim([-300,300])
# define function for vertical plots
def vert_cross(yaw_angles, diameter, x_spacing):
# calculate lagged wakes for vertical profiles
fi.calculate_wake(yaw_angles=yaw_angles)
cross_sections['cross_section_%s' %idx] = fi.get_cross_plane(((x_spacing) * idx * diameter) - diameter, z_bounds=(0,300), y_bounds=(-200,200))
img = wfct.visualization.visualize_cut_plane(cross_sections['cross_section_%s' %idx], ax=wake_profiles['wake_profile_%s' %idx], minSpeed=6.0, maxSpeed=8)
wake_profiles['wake_profile_%s' %idx].set_ylim([0, 300])
# reverse cut so looking down-stream
wfct.visualization.reverse_cut_plane_x_axis_in_plot(wake_profiles['wake_profile_%s' %idx])
# apply centeral heading
if idx == 2: #assume at lead three agents
wake_profiles['wake_profile_%s' %idx].set_title('Vertical Cross Sections of Wake Profiles',fontsize=8, fontweight='bold')
# plot line on plan vis to show vertical slice
trb_plan.plot([((x_spacing) * idx * diameter) - diameter, ((x_spacing) * idx * diameter) - diameter], [-500, 500], 'k', linestyle='dashed', lw=0.6)
# get current vertical slice distance in diameters
current_dia = (((x_spacing) * idx * diameter) - diameter) / diameter
# apply some formatting to the graphs
wake_profiles['wake_profile_%s' %idx].set_xticklabels([])
wake_profiles['wake_profile_%s' %idx].set_xlabel('{}D'.format(current_dia), fontsize=9, style='italic')
wake_profiles['wake_profile_%s' %idx].set_yticklabels([])
wake_profiles['wake_profile_%s' %idx].set_yticks([])
# plot line on plan vis to show vertical slice
wake_profiles['wake_profile_%s' %idx].plot([0, 0], [-500, 500], 'k', linestyle='dashed', lw=0.4, alpha=0.4)
# reinstate current yaws
fi.calculate_wake(yaw_angles=list(data['windfarm_yaws']))
# update vertical cross sections with time dealys
for idx in range(1, agents+1):
if idx <= 2 and data['locked_turb'][idx] == False:
vert_cross(list(data['prev_windfarm_yaws']), diameter, x_spacing)
elif data['out_wake_delays'] <= -1.0 and idx == 3:
vert_cross(list(data['prev_windfarm_yaws']), diameter, x_spacing)
elif idx <= 2 and data['locked_turb'][idx] == True:
vert_cross(list(data['intial_windfarm_yaws']), diameter, x_spacing)
elif data['out_wake_delays'] > -1.0 and idx == 3:
vert_cross(list(data['intial_windfarm_yaws']), diameter, x_spacing)
# first line graph - Power + wind speed
wf_pwr_line.set_data(time_all, windfarm_power_all)
wf_pwr_line_sec.set_data(time_all, ws_all)
# second line graph - Turbine Yaw Angles + reward
for line, key in enumerate(turbine_yaws_all.keys()):
turb_yaw_lines[line].set_data(time_all, turbine_yaws_all[key])
trb_yaws_sec.set_data(time_all, reward_all)
# third line graph turbine powers - left axis first turbine, then others on right
trb_pwrs_line.set_data(time_all, first_turbine_powers_all) # left axis first turbine
for line, key in enumerate(turbine_powers_all.keys()): # right axis other turbines
sec_trb_pwrs_lines[line].set_data(time_all, turbine_powers_all[key])
return [wf_pwr_line, trb_yaw_line, trb_pwrs_line]
animation_ = FuncAnimation(fig, update, interval=24, blit=True, save_count=10)
plt.show(block=True)
animation_.save('floris_animation.gif', writer='imagemagick', fps=20)
# FFwriter = animation.FFMpegWriter(fps=20, codec="libx264")
# animation_.save('test.mp4', writer = FFwriter)
# fig.savefig('floris_final_still.jpg', bbox_inches='tight')